TÍNH KHUNG SIÊU TĨNH BẰNG PHƯƠNG PHÁP LỰC
Mọi ý kiến đóng góp xin gửi vào hòm thư: [email protected]
Kéo xuống để Tải ngay đề cương bản PDF đầy đủ: Sau “mục lục” và “bản xem trước”
(Nếu là đề cương nhiều công thức nên mọi người nên tải về để xem tránh mất công thức)
Đề cương liên quan: Bài tập lớn môn Điều khiển số Thiết kế theo tiêu chuẩn tích phân số (IAE, ITAE, ISE, ITSE) kết hợp với Dead – Beat khâu điều chỉnh tốc độ động cơ DC Servo Harmonic RHS 17 – 6006
Mục Lục
- TÍNH KHUNG SIÊU TĨNH BẰNG PHƯƠNG PHÁP LỰC
- YÊU CẦU VÀ THỨ TỰ THỰC HIỆN
- 1. Tính hệ siêu tĩnh do tải trọng tác dụng.
- 3. Tính hệ siêu tĩnh chịu tác dụng cả 3 nguyên nhân (Tải trọng, nhiệt độ thay đổi và chuyển vị gối tựa).
- SƠ ĐỒ TÍNH KHUNG SIÊU TĨNH
- BÀI LÀM
- 1.Tính hệ siêu tĩnh do tải trọng tác dụng.
- Tải xuống tài liệu học tập PDF miễn phí
Tải ngay đề cương bản PDF tại đây: TÍNH KHUNG SIÊU TĨNH BẰNG PHƯƠNG PHÁP LỰC
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
TÍNH KHUNG SIÊU TĨNH BẰNG PHƯƠNG PHÁP LỰC
Số liệu như sau :
|
Kích thước hình học |
Tải trọng |
||||
|
STT |
L1 |
L2 |
q(kN/m) |
P (kN) |
M(kN/m) |
|
1 |
10 |
8 |
40 |
100 |
120 |
YÊU CẦU VÀ THỨ TỰ THỰC HIỆN
1. Tính hệ siêu tĩnh do tải trọng tác dụng.
1.1. Vẽ các biểu đồ nội lực: Momen uốn MP , lực cắt QP , lực dọc NP trên hệ siêu tĩnh đã cho. Biết F = 10J/L12 (m2)
1.Xác định bậc siêu tĩnh và chọn hệ cơ bản.
2.Thành lập các phương trình chính tắc dạng tổng quát.
3.Xác định các hệ số và số hạng tư do của phương trình chính tắc, kiểm tra các kết quả tính toán.
4.Giải hệ phương trình chính tắc.
5.Vẽ biểu đồ mômen MP trên hệ siêu tĩnh đã cho do tải trọng tác dụng. Kiểm tra cân bằng các nút và kiểm tra điều kiên chuyển vị.
6.Vẽ biểu đồ lực cắt QP và lực dọc NP trên hệ siêu tĩnh đã cho.
1.2. Xác định chuyển vị ngang tại mặt cắt I(trọng tâm). Biết E = 2.108 kN/m2 , J = 10-6 L41 (m4)
3. Tính hệ siêu tĩnh chịu tác dụng cả 3 nguyên nhân (Tải trọng, nhiệt độ thay đổi và chuyển vị gối tựa).
2.1. Viết và giải hệ phương trình chính tắc dạng số
2.2. Thứ tự thực hiện
- Vẽ biểu đồ momen uốn M do 3 nguyên nhân đồng thời tác dụng trên hệ siêu tĩnh đã cho và kiểm tra kết quả.
- Tính các chuyển vị như đã nêu ở mục 1.2
Biết :
-Nhiệt độ trong thanh xiên: thớ biên trên là Ttr = +45o ,thớ biên dưới là Td =+30o -Thanh xiên có chiều cao mặt cắt h=0,12 m
-Hệ số dãn nở vì nhiệt của vật liệu
-Chuyển vị gối tựa
Gối D dịch chuyển sang phải một đoạn D1 = 0,001L1 (m)
Gối H bị lún xuống đoạn D2 = 0,001L2 (m)
SV: Đào Thị Bính 1 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
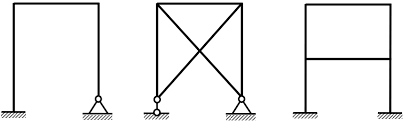
SƠ ĐỒ TÍNH KHUNG SIÊU TĨNH
q
|
I |
||||
|
6m |
F |
M |
||
|
2J |
||||
|
P |
||||
|
2J |
P |
3J |
||
|
8m |
J |
J |
||
|
H |
D |
|||
|
10m |
8m |
10m |
SV: Đào Thị Bính 2 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
BÀI LÀM
1.Tính hệ siêu tĩnh do tải trọng tác dụng.
1.1. Vẽ các biểu đồ nội lực: Momen uốn MP, lực cắt QP, lực dọc NP trên hệ siêu tĩnh đã cho. Biết F = 10J/L12 (m2).
- Xác định bậc siêu tĩnh và chọn hệ cơ bản:
- Xác định bậc siêu tĩnh :
Gọi n là số liên kết thừa.
Hệ kết cấu có 2 chu vi kín và 3 khớp đặt vào hệ.
Ta có n = 3V – K trong đó : V là số chu vi kín ( V = 2 )
K là số khớp đặt vào hệ ( K =3 )
Vậy n = 3.2 – 3 = 3
Vậy đây là hệ siêu tĩnh bậc 3 .
+ Chọn hệ cơ bản:
q
|
I |
|||||
|
6m |
X3 |
X1 |
X1 |
||
|
2J |
M |
||||
|
X2 |
X2 |
||||
|
P |
2J |
P |
3J |
||
|
8m |
J |
J |
|||
|
X3 |
|||||
|
H |
D |
||||
|
10m |
8m |
10m |
|||
2.Thành lập các phương trình chính tắc dạng tổng quát.
Đối với hệ có thể áp dụng nguyên lý cộng tác dụng , với những hệ này ta có thể biểu thị phương trình cơ bản . Hệ siêu tĩnh bậc n thì có n điều kiện chuyển vị.
Tại liên kết thứ i đã bỏ đi điều kiên chuyển vị là : i = 0 i = (Xi , Xk , P , t , z ) = 0
- chuyển vị theo phương Xi do Xi =1 gây ra . ik chuyển vị theo phương Xi do Xk =1 gây ra .
iP chuyển vị theo phương Xi do P tải trọng gây ra . it chuyển vị theo phương Xi do nhiệt độ gây ra .
iz chuyển vị theo phương Xi do độ lún gây ra .
chuyển vị theo phương Xi do độ dôi gây ra .
Vậy phương trình cơ bản thứ i có dạng như sau :
ii . Xi + ik . Xk + iP + it + iz + = 0 ( i,k =1 n )
SV: Đào Thị Bính 3 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
Với n bậc siêu tĩnh sau khi cho lần lượt i = 1 , 2 , 3 … , n ta sẽ có n phương trình cơ bản của phương pháp lực .
Hệ phương trình chính tắc dạng tổng quát của phương pháp lực có dạng như sau:
d11 X1 + d12 X 2 + d13 X 3 + … + d1 n X n + D1 P + D1 z + D1t + D1 D = 0
- 21 X1 + d 22 X 2 + d 23 X 3 + … + d 2 n X n + D2 P + D 2 z + D 2 t + D 2 D = 0
………………………………………………………………..
- n1 X1 + d n 2 X 2 + d n 3 X 3 + … + d nn Xn + D nP + D nz + D nt + D n D = 0
Giải hệ phương trình chính tắc Xi (i = 1 n )
ii hệ số chính
ik hệ số phụ ( i k )
iP , it , iz , là các số hạng tự do
- trường hợp này n = 3 và chỉ xét hệ siêu tĩnh do tải trọng gây ra, không có các chuyển vị do nhiệt độ, độ dôi,do gối tựa bi lún. Nên ta được các phương trình chính tắc như sau:
ìd X + d X + d X + D = 0
ï 11 1 12 2 13 3 1 P
íd 21 X 1 + d 22 X 2 + d23 X 3 + D 2 P = 0
ï
îd 31 X 1 + d 32 X 2 + d33 X 3 + D 3 P = 0
3.Xác định các hệ số và số hạng tư do của phương trình chính tắc, kiểm tra các kết quả tính được .
Vẽ các biểu đồ momen do các lực X1=1, X2=1 và X3=1 gây ra trên hệ.
+Vẽ biểu đồ momen và lực dọc do lực X1=1 gây ra trên hệ cơ bản:
Biểu đồ momen :
X1=1
X1=1
6
M 1
kNm
|
14 |
14 |
SV: Đào Thị Bính 4 Lớp: XDCTN & mỏ k54
|
BÀI TẬP LỚN |
Môn : Cơ học kết cấu 2 |
|
Biểu đồ lực dọc : |
|
|
1 |
1 |
N1
kNm
+Vẽ biểu đồ momen do lực X2=1 gây ra trên hệ cơ bản:
X2=1 X2 =1
M 2
kNm
|
8 |
8 |
||||
|
+Vẽ biểu đồ momen |
do lực X3=1 gây ra trên hệ cơ bản: |
||||
X3=1 10
|
10 |
M 3 |
|
|
X3=1 |
||
|
kNm |
||
|
10 |
SV: Đào Thị Bính 5 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
+Vẽ biểu đồ momen do tải trọng q, lực P và momen M gây ra trên hệ :
40kN/m
120kNm
100kN
100kN
Biểu đồ nội lực:
120
1600
MP0
kNm
800 2400
Xác định các hệ số và số hạng tự do trọng hệ phương trình chính tắc:
|
11 = |
+ |
= |
( |
8.8. |
+ 6.8 10) + |
. 6.10. |
.6 + |
.14.14. |
.14 |
||||||||||||||||||||||||||||||||||||||||||||
|
+ |
.1.10.10 = |
+ |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
. ( |
8.8. |
.8 + 6.8. |
8 ) = |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
12 = |
21 = |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
.8.10 = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
13 = |
31 = |
. |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||
SV: Đào Thị Bính 6 Lớp: XDCTN & mỏ k54
|
BÀI TẬP LỚN |
Môn : Cơ học kết cấu 2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
22 = |
= |
.8.8. |
.8.2 = |
||||||||||||||||||||||||||||||||||||||||||||||||
|
.8.8.10 = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
23 = |
32 = |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
33 = |
= |
. |
10.10. |
.10 + |
10.8.10 = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1P = |
. |
.800.8. |
+ 1600.8.10 + |
. |
1600.10. |
.6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
.120.14. |
.14 = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2P = |
.800.8. |
.8 |
.800.8. |
.8 |
1600.8. |
.8 ) = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3P = |
. |
.8.10 = |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Kiểm tra các kết quả tính toán: |
||||
|
+ Kiểm tra các biểu đồ |
(i= |
) |
||
|
Ta có: |
||||
- ∑
Biểu đồ momen uốn tổng :
SV: Đào Thị Bính 7 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
+ Kiểm tra các hệ số của ẩn số trong hệ phương trình:
|
· Theo hàng thứ nhất. Nhân |
: |
|||||||||||||||||||||||||||||||||||
|
= |
. 16.8.10 + |
. 6.10. |
.6 + |
.14.14. |
.14 |
|||||||||||||||||||||||||||||||
|
Mặt khác ta có: |
||||||||||||||||||||||||||||||||||||
|
11 + 12 + |
13 = |
+ |
+ |
= |
+ |
(đúng) |
||||||||||||||||||||||||||||||
Chuyển vị do lực dọc gây ra là rất nhỏ so với momen nên ta coi như bằng 0
|
· Theo hàng thứ hai. Nhân |
: |
||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
( |
8.8. |
.8 – 16.8 |
.8 ) = |
|||||||||||||||||||||||||||||||||||||||||||||
|
Mặt khác ta có: |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
12 + |
22 + |
23 |
= |
= |
(đúng) |
||||||||||||||||||||||||||||||||||||||||||||
|
· Theo hàng thứ ba. Nhân |
: |
||||||||||||||||||||||||||||||||||||||||||||||||
|
10.10. |
.10 |
16.8.10 = |
|||||||||||||||||||||||||||||||||||||||||||||||
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Mặt khác ta có: |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
13 + |
23 + |
33 |
= |
= |
(đúng) |
||||||||||||||||||||||||||||||||||||||||||||
- Kiểm tra tất cả các hệ số của ẩn số: Ta có:
∑
= .( 8.8. .8 + 16.8.16) + .( 10.10. .10 + .6.10. .6)
- .14. .14 =
Mặt khác ta có:
11 + 12 + 13 + 21 + 22 + 23 + 31 + 32 + 33 = +
+ =
- Kiểm tra tất cả các số hạng tự do do tải trọng gây lên:
Ta có:
∑
SV: Đào Thị Bính 8 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
|
.800.8. |
.8 + |
.8.16) + |
. |
1600.10. |
.6 |
||||||||||
|
= |
|||||||||||||||
.120.14. .14 =
Mặt khác ta có:
1P + 2P + 3P = + = (đúng)
Các hệ số và số hạng tự do đã tính đúng.
4.Giải hệ phương trình chính tắc.
Thay các hệ số vừ tính được vào hệ phương trình chính tắc sau:
ìd X + d X + d X + D = 0
ï 11 1 12 2 13 3 1 P
íd 21 X 1 + d 22 X 2 + d23 X 3 + D 2 P = 0
Ta được hệ phương trình sau:
{
Giải hệ phương trình chính tắc trên ta được các ẩn lực:
{
5.Vẽ biểu đồ mômen trên hệ siêu tĩnh đã cho do tải trọng tác dụng MP. Kiểm tra cân bằng các nút và kiểm tra điều kiên chuyển vị.
- Vẽ biểu đồ momen trên hệ siêu tĩnh đã cho do tải trọng tác dụng MP:
MP = X1 + .X2 + .X3 +
SV: Đào Thị Bính 9 Lớp: XDCTN & mỏ k54
|
BÀI TẬP LỚN |
Môn : Cơ học kết cấu 2 |
|
|
Biểu đồ |
X1: |
|
|
193,4052 |
||
|
193,4052 |
(M1).X1 |
|
|
kNm |
||
451,2788
Biểu đồ X2:
193,4052
|
193,4052 |
(M1).X1 |
kNm
451,2788
Biểu đồ X3:
1457,584
1457,584
(M3).X3
kNm
1457,584
SV: Đào Thị Bính 10 Lớp: XDCTN & mỏ k54
|
BÀI TẬP LỚN |
Môn : Cơ học kết cấu 2 |
||
|
Biểu đồ momen MP: |
|||
|
1457,584 |
120 |
||
|
1406,5948 |
5,84462 |
||
|
50,9892 |
|||
|
MP |
|||
|
kNm |
|||
|
632,8216 |
658,3156 |
571,2788 |
|
+Kiểm tra cân bằng các nút:
Nút 1:
0
0
Nút 2:
1406,5948
1457,584
50,9892
Nút 3:
0
0
SV: Đào Thị Bính 11 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
Nút 4:
120
120
+Kiểm tra điều kiện chuyển vị:
Ta có:
.632,8216.8. .8 .50,9892.0,5751.16+ .658,3156.7,4249.16)
. 1457,584.10. .10
+ .( 4,681305) .0,36261
.( .451,2788.14. .14+120.14. .14)
Với E = 2.108 kN/m2 , J = 10-6 104 (m4)
Ta có:
Ta thấy chuyển vị rất nhỏ nên có thể coi bằng 0 và do sai số trong tính toán gây nên. Điều đó chứng tỏ MP vẽ đúng.
6.Vẽ biểu đồ lực cắt QP và lực dọc NP trên hệ siêu tĩnh đã cho.
Biểu đồ lực cắt:
120,6594
160,6595
Q P
145,758 kNm
|
79,1027 |
88,6631 |
32,2342 |
SV: Đào Thị Bính 12 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
Tách nút:
|
160,6595 |
265,78736 |
||
|
100 |
20,8973 |
20,8973 |
|
|
32,2342 |
|||
|
145,758 |
145,758 |
||
|
79,1027 |
88,6631 |
32,2342 |
|
|
145,758 |
545,7584 |
||
Biểu đồ lực dọc:
25,78736
265,78736
32,2342
N P
kNm
20,8973
145,758 545,7584
1.2. Xác định chuyển vị ngang tại mặt cắt I(trọng tâm. Biết E = 2.108 kN/m2 J = 10-6 L41 (m4)
|
+Lập trạng thái phụ “k” và vẽ biểu đồ momen |
khi đặt một lực Pk=1 vào hệ tĩnh |
|
|
định được suy ra từ hệ siêu tĩnh (n=3) |
SV: Đào Thị Bính 13 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
I
|
Pk =1 |
F |
M |
2J
2J
3J
J J
|
H |
D |
Vẽ biểu đồ :
6
|
6 |
M k |
|
kNm |
14
+Trạng thái “m” chính là nội lực và chuyển vị trong hệ cơ bản tĩnh định chịu tác dụng của các ẩn lực là biểu đồ MP:
120
1457,584
|
1406,5948 |
5,84462 |
|
|
50,9892 |
||
|
MP |
||
|
kNm |
||
|
632,8216 |
658,3156 |
571,2788 |
|
Chuyển vị ngang tai I: |
||||||||||||||||
|
kP=MP.Mk= |
.50,9892.0,58.16 |
.658,3156.( |
.7,42)) |
|||||||||||||
|
.( |
4,68) |
.0,36 = 5,735.10-3 |
||||||||||||||
Dấu “ “ chứng tỏ điểm I sẽ dịch chuyển sang phai một đoạn 0,5735 (cm)
SV: Đào Thị Bính 14 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
- Tính hệ siêu tĩnh chịu tác dụng cả 3 nguyên nhân (Tải trọng, nhiệt độ thay đổi và chuyển vị gối tựa).
2.1. Viết hệ phương trình chính tắc dạng số Ta biết:
-Nhiệt độ trong thanh xiên: thớ biên trên là Ttr = +45o ,thớ biên dưới là Td =+30o -Thanh xiên có chiều cao mặt cắt h=0,12 m
-Hệ số dãn nở vì nhiệt của vật liệu -Chuyển vị gối tựa
Gối D dịch chuyển sang phải một đoạn D1 = 0,001L1 (m)
Gối H bị lún xuống đoạn D2 = 0,001L2 (m)
Chọn hệ cơ bản giống như phần 1:
Hệ phương trình chính tắc của hệ chịu tác dụng của cả 3 nguyên nhân tải trọng , nhiệt độ thay đổi va chuyển vị gối tựa:
ìïd11 . X 1 + d12 . X 2 + d13 . X 3 + D1 p + D1t + D1 z = 0 íd 21 . X 1 + d 22 . X 2 + d23 . X3 + D 2 p + D 2 t + D 2 z = 0 ïîd 31 . X 1 + d 32 . X 2 + d33 . X 3 + D 3 p + D 3 t + D 3 z = 0
2.2. Thứ tự thực hiện
- Vẽ biểu đồ momen uốn M do 3 nguyên nhân đồng thời tác dụng trên hệ siêu tĩnh đã cho và kiểm tra kết quả.
Ta tính các hệ số do tác động của nhiệt độ gây nên:
∑ ̅ ∑ ̅
Ta có biểu đồ lực dọc:
SV: Đào Thị Bính 15 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
+Biểu đồ lực dọc :
0,8 X1=1
X1=1
0,8
N 1
kNm
+Biểu đồ lực dọc :
X2=1 X2 =1
1
N 2
kNm
+Biểu đồ lực dọc :
|
X3=1 |
|
|
1 |
1 |
|
N 3 |
|
|
X3=1 |
kNm |
|
1 |
1 |
Sử dụng các biểu đồ M1, M2, M3 ở phần 1 nên hệ số của ẩn số giống hệ phương trình ở phần 1.
Xác định các số hạng tự do của phương trình chính tắc:
SV: Đào Thị Bính 16 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
1P =
2P =
3P =
|
1t = |
= 0,0255 |
|||
|
2t = |
3t = 0 |
|||
|
X1 |
làm gối D dịch chuyển sang phải một đoạn 1 |
|||
|
X3 |
làm gối H lún một đoạn 2 |
|||
|
Vậy: |
iz = |
|||
|
Tích số |
mang dấu + do phản lực cùng chiều với chuyển vị. |
|||
|
1z |
= |
1.0,01 = |
0,01 |
|
|
2z |
= |
1.0,008 = |
0,008 |
|
Vậy ta có hệ phương trình sau:
{
Giải hệ phương trình chính tắc trên ta được các ẩn lực:
{
Vẽ biểu đồ mômen trên hệ siêu tĩnh đã cho do tải trọng , nhiệt độ và chuyển vị gối tựa gây nên MP.
+ Vẽ biểu đồ momen trên hệ siêu tĩnh đã cho do tải trọng tác dụng MP:
MP = X1 + .X2 + .X3 +
SV: Đào Thị Bính 17 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
Biểu đồ X1:
1126,9812
(M1).X1
kNm
|
2629,6228 |
2629,6228 |
Biểu đồ X2:
(M2).X2
kNm
744,5352 744,5352
Biểu đồ X3:
2736,028
2736,028
(M3).X3
kNm
2736,028
SV: Đào Thị Bính 18 Lớp: XDCTN & mỏ k54
|
BÀI TẬP LỚN |
Môn : Cơ học kết cấu 2 |
|
|
Biể đồ MP: |
||
|
120 |
||
|
1457,584 |
||
|
1406,5948 |
5,84462 |
|
50,9892
MP
kNm
632,8216 658,3156 2509,6228
+Kiểm tra cân bằng các nút:
Nút 1:
0
0
Nút 2:
2726,9812
2736,028
9,0468
Nút 3:
0
0
SV: Đào Thị Bính 19 Lớp: XDCTN & mỏ k54
BÀI TẬP LỚN Môn : Cơ học kết cấu 2
Nút 4:
120
120
2.Xác định chuyển vị ngang tại mặt cắt I chịu tác dụng cả 3 nguyên nhân (Tải trọng, nhiệt độ thay đổi và chuyển vị gối tựa). Lập trạng thái phụ “k”:
Biểu đồ momen ở trạng thái “k”
6
|
6 |
M k |
|
kNm |
14
Biểu đồ momen ở trạng thái “m”
SV: Đào Thị Bính 20 Lớp: XDCTN & mỏ k54
|
BÀI TẬP LỚN |
Môn : Cơ học kết cấu 2 |
||||
|
1457,584 |
120 |
||||
|
1406,5948 |
5,84462 |
||||
|
50,9892 |
|||||
|
MP |
|||||
|
kNm |
|||||
|
632,8216 |
658,3156 |
2509,6228 |
|||
|
= |
kP + |
+ |
|||
|
Trong đó: |
= 0,0255 |
||||
|
= |
0,008 |
0,01 = 0,018 |
|||
|
kP = MP.Mk = |
.0,046.9,0468.6,015 |
.1549,0596.9,954.10,682) |
|||
|
. |
5,55 + |
.2,1 = |
0,044 |
||
|
= kP + |
+ |
= |
0,044 + 0,0255 |
0,018 = |
0,0365m |
MP là biểu đồ momen trên hệ siêu tĩnh dưới tác động đồng thời của tải trọng, nhiệt độ và chuyển vị cưỡng bức của gối tựa.
Mk là biểu đồ momen ở trạng thái “k” dưới tác động đồng thời của tải trọng, nhiệt độ và chuyển vị cưỡng bức của gối tựa.
Dấu “ ” chứng tỏ chuyển vị ngược chiểu với Pk=1 một khoảng: 3,65 (cm)
SV: Đào Thị Bính 21 Lớp: XDCTN & mỏ k54