Khảo sát rẽ nhánh của dao động tuần hoàn trong hệ tuyến tính từng khúc bằng phương pháp bắn đơn
Mọi ý kiến đóng góp xin gửi vào hòm thư: [email protected]
Kéo xuống để Tải ngay đề cương bản PDF đầy đủ: Sau “mục lục” và “bản xem trước”
(Nếu là đề cương nhiều công thức nên mọi người nên tải về để xem tránh mất công thức)
Đề cương liên quan: Quyền dự phòng và chuyển quyền dự phòng của các tổ hợp DG tàu thuỷ
Mục Lục
Tải ngay đề cương bản PDF tại đây: Khảo sát rẽ nhánh của dao động tuần hoàn trong hệ tuyến tính từng khúc bằng phương pháp bắn đơn
KHẢO SÁT RẼ NHÁNH CỦA DAO DỘNG TUẦN HOÀN TRONG HỆ TUYẾN TÍNH TỪNG KHÚC BẰNG PHƯƠNG PHÁP BẮN ĐƠN ANALYZING THE BIFURCATION OF PERIODIC VIBRATIONS OF PIECEWISE-LINEAR SYSTEMS USING THE SINGLE SHOOTING METHOD
- HOÀNG MẠNH CƯỜNG
Viện Khoa học cơ sở, Trường ĐHHH Việt Nam
- LÊ ANH TUẤN
Khoa Cơ khí, Trường ĐHHH Việt Nam
Tóm tắt
Trong bài báo này, đã áp dụng phương pháp bắn đơn trong việc tính toán dao động tuần hoàn của hệ dao động cưỡng bức chịu kích động điều hòa. Sự không đối xứng của hệ khảo sát dẫn đến cả độ cứng và độ cản nhớt là các hàm tuyến tính tứng khúc. Việc phân tích ổn định và rẽ nhánh của hệ dao động phi tuyến đã được tiến hành bằng phương pháp tính toán số. Từ các phân tích cho thấy rằng, trong hệ khảo sát xuất hiện các rẽ nhánh nhân đôi chu kỳ và sự tồn tại đồng thời của nhiều tập hút tuần hoàn.
Abstract
This article analyses the periodic vibration of harmonically excited systems using the single shooting method. Both stiffness and viscous damping are piecewise-linear functions due to non-symmetry of system. Analyzing the stability and bifurcation of nonlinear systems are carried out by numerical method. The analysis results show the existence of period-doubling bifurcation and multiple periodic attractors.
Key words: Nonlinear vibration, shooting method, Bifurcation.
1. Mở đầu
Trong các hệ dao động máy như các bánh răng chịu tải trọng nhẹ, các hệ rotor, các hệ dao động đàn hồi, các hệ cam-cần cam, các khớp liên kết các thành phần robotic, … tính chất tuyến tính hoặc phi tuyến từng khúc tồn tại vì khe hở giữa các thành phần. Các hệ tuyến tính từng khúc là các hệ phi tuyến mạnh, để tính toán dao động của các hệ này ta có thể sử dụng phương pháp cân bằng điều hòa gia lượng [2, 3, 4, 6]. Nhưng để đạt được độ chính xác cao, phương pháp này đòi hỏi số các thành phần điều hòa trong biểu thức nghiệm phải lớn, điều này dẫn đến ta phải giải một hệ nhiều phương trình đại số phi tuyến, đây là vấn đề rất khó khăn. Để khắc phục hạn chế này, phương pháp bắn đơn [1] tỏ ra có ưu thế hơn, vì trong phương pháp này số phương trình của hệ đại số phi tuyến chỉ tương ứng với số chiều của hệ, do đó sẽ giảm khối lượng tính toán và tăng độ chính xác của nghiệm thu được.
Trong bài báo này, đã xây dựng thuật toán khảo sát sự ổn định và rẽ nhánh của nghiệm tuần hoàn trong các hệ phi tuyến không ôtônôm, dựa trên phương pháp bắn đơn. So sánh các kết quả tính toán với các kết quả tính bằng phương pháp cân bằng điều hòa gia lượng [6], cho thấy các kết quả hoàn toàn tương tự. Việc đưa ra thuật toán tính toán số trong bài bào này có thể dễ dàng được áp dụng để phân tích các ứng sử động lực học phức tạp như rẽ nhánh và dao động hỗn độn của các hệ kỹ thuật trong thực tế.
Tạp chí Khoa học Công nghệ Hàng hải Số 39 – 08/2014 30
2. Phương pháp bắn đơn tìm nghiệm tuần hoàn của các hệ không ôtônôm
Cho hệ phương trình vi phân không ôtônôm (thêm dấu : )
x = f ( x, t, μ) (1)
Trong đó x Î n , f Î n , m là các tham số, f(x,t,m) là hàm tuần hoàn chu kỳ Te. Bài toán đặt
ra là, ta phải đi tìm nghiệm tuần hoàn chu kỳ T của hệ (1), nghĩa là ta phải đi tìm nghiệm của hệ (1) sao cho thoả mãn điều kiện x(0) = x(T). Ta đã biết, đối với các hệ không ôtônôm, chu kỳ T của nghiệm tuần hoàn cần tìm là một bội số hữu tỷ của Te và là một số đã biết. Do đó, để thực hiện phương pháp bắn tìm nghiệm tuần hoàn chu kỳ T của hệ (1), trước tiên, ta xét bài toán (thêm : )
- = f ( x, t, μ)
với điều kiện đầu
x(0) =
η
,
(2)
sau đó, ta phải đi tìm điều kiện đầu kiện (thêm dấu : )
x(T , η) = x (0) = η Û x(T, η) –
- sao cho nghiệm x(t,h) của bài toán (2) thoả mãn điều
|
η = 0 |
(3) |
- là hệ n phương trình đại số phi tuyến với n ẩn số là hk (k =1, 2, …, n). Để giải hệ phương trình đại số này ta có thể sử dụng các phương pháp lặp, như phương pháp Newton-Raphson được trình bày dưới đây:
Ban đầu ta cho một sự ước chừng điều kiện đầu h(0) và mong muốn tìm được h, sao cho sai lệch dh = h – h(0) thoả mãn điều kiện ||dh|| < e, với e là một số nhỏ cho trước, để mà (thêm dấu : )
x(T , η(0) + d η) – ( η(0) + d η) » 0
Khai triển Taylor đối với (4) và chỉ giữ lại
(4)
các số hạng tuyến tính đối với dh, ta được (thêm : )
|
é ¶x |
(0) |
ù |
(0) |
(0) |
|||||
|
ê |
(T , η |
) – E |
ú |
d η = η |
– x (T , η |
) |
|||
|
¶η |
|||||||||
|
ë |
û |
||||||||
(5)
trong đó E là ma trận đơn vị cấp n´n, x(T,h(0)) là véc tơ có n phần tử và được xác định bằng cách giải bài toán điều kiện đầu (2) trong khoảng thời gian t = [0, T]. Còn ¶x/¶h là ma trận cấp n´n các thành phần của ma trận này tại (T,h(0)) được xác định như sau: Đạo hàm hai vế phương trình
- theo h, ta được (thêm dấu : )
|
d æ |
¶x ö |
= Dxf ( x, t, μ) |
¶x |
(6) |
||
|
ç |
÷ |
|||||
|
¶η |
||||||
|
dt è |
¶η ø |
|||||
Ngoài ra đạo hàm của điều kiện đầu x(0) = h đối với h, ta được (thêm dấu : )
|
¶x |
(0) = E |
(7) |
|
|
¶η |
|||
- là phương trình vi phân đối với ¶x/¶h, tích phân phương trình (6) với điều kiện đầu (7) trong khoảng thời gian t = [0, T], ta được ¶x/¶h tại (h(0), T). Khi ma trận ¶x/¶h được xác định thì hệ
- trở thành hệ n phương trình đại số tuyến tính với các ẩn số là dh. Sau khi giải hệ (5), ta kiểm tra tiêu chuẩn hội tụ ||dh|| < e. Nếu tiêu chuẩn hội tụ không được thoả mãn, ta cập nhật lại điều kiện đầu h(0) = h(0) + dh và quay lại các bước ở trên cho đến khi các tiêu chuẩn hội tụ được thoả mãn. Kết thúc thủ tục ta tìm được điều kiện đầu h tương ứng với nghiệm tuần hoàn chu kỳ T của hệ (1).
3. Khảo sát rẽ nhánh của các hệ phi tuyến bằng phương pháp số
- Bước 1: Chọn giá trị đầu m = m0. Bằng phương pháp bắn, ta tìm điều kiện đầu h0 và chu kỳ T0 ứng với nghiệm tuần hoàn (x(t, h0, T0), m0) của hệ (1), giả sử nghiệm này ổn định.
- Bước 2: Chọn số gia Dm thích hợp, lấy m = m0 + Dm
- Bước 3: Lấy (h0, T0) làm giá trị khởi đầu cho phương pháp bắn, tìm điều kiện đầu h và chu kỳ T của nghiệm tuần hoàn x(t, h, T) của hệ (1) tại m = m0 + Dm.
- Bước 4: Tích phân số phương trình (1) với điều kiện đầu h, ta được nghiệm tuần hoàn x(t, h, T). Kiểm tra các nhân tử Floquet ứng với nghiệm này. Nếu tất cả các nhân tử Floquet đều nằm trong vòng tròn đơn vị của mặt phẳng phức thì nghiệm này là ổn định, ta cập nhật lại các giá trị
Tạp chí Khoa học Công nghệ Hàng hải Số 39 – 08/2014 31
khởi đầu m0 = m, h0 = h, T0 = T và ta quay lại từ bước 2. Nếu có nhân tử Floquet nằm trên vòng tròn đơn vị của mặt phẳng phức và nhân tử này đang có xu hương đi ra khỏi vòng tròn đơn vị, thì ta có giá trị rẽ nhánh m và tiếp tục từ bước 5.
* Bước 5: Kiểm tra hướng của nhân tử Floquet dời khỏi vòng tròn đơn vị của mặt phẳng
phức
- Nếu nhân tử Floquet là số thực, dời vòng tròn đơn vị theo hướng -1, ta có rẽ nhánh nhâ đôi chu kỳ (thêm dấu . )
- Nếu nhân tử Floquet là số thực, dời vòng tròn đơn vị theo hướng +1, ta có một trong các rẽ nhánh: nếp gấp-chu trình, rẽ nhánh chuyển qua giới hạn, rẽ nhánh phá huỷ tính đối xứng.
- Nếu nhân tử Floquet là số phức dời vòng tròn đơn vị , ta có rẽ nhánh Hopf loại 2.
4. Tính toán dao động tuần hoàn và khảo sát rẽ nhánh của hệ tuyến tính từng khúc
4.1. Mô hình động lực học của tuyến tính từng khúc
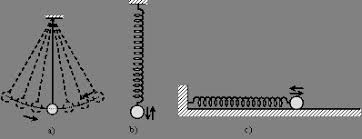
Cho mô hình dao động như hình 1, trong đó khối lượng m được nối với lò xo k0 và cản nhớt c0, lò xo k1 và cản nhớt c1 được để tự do. Giả thiết rằng khi không có khối lượng m, hai lò xo tự do chạm nhau, khi có khối lượng m, tại vị trí cân bằng tĩnh các lò xo với các độ cứng tương ứng k0, k1 bị nén một đoạn tương ứng là d0 và d. Cho khối lượng m chịu tác dụng của lực kích động điều hoà f0sinWt. Gọi x là dịch chuyển của cạnh bên phải khối lượng m đối với vị trí của cạnh bên phải của khối lượng tại vị trí cân bằng tĩnh.
f0
Hình 1. Mô hình dao động của hệ
tuyến tính từng khúc
Phương trình vi phân dao động của hệ này có dạng (thêm dấu : )
mx + c0 x + k0 x + c0 H ( x) + G( x) = f 0 sin Wt
trong đó (thêm dấu : )
|
ìc x / c |
, |
x > –d |
ìk x , |
x > –d |
||||||
|
H (x) = í |
1 |
0 |
; |
G (x) = í |
1 |
|||||
|
0, |
x £ –d |
– k 0 |
d 0 |
, |
x £ –d |
|||||
|
î |
î |
|||||||||
Bằng cách đặt x1 = x, x2 = dx/dt, từ (8) ta có (thêm dấu : )
|
ìx |
= x |
|||||||||
|
ï |
1 |
2 |
||||||||
|
í |
x |
= [ – c x |
– k x |
– c H (x |
) – G (x ) + f |
sin Wt ] / m |
||||
|
ï |
||||||||||
|
2 |
0 |
2 |
0 |
1 |
0 |
2 |
1 |
0 |
||
|
î |
||||||||||
trong đó (thêm dấu : )
(8)
(9)
|
ìc x |
2 |
/ c |
, |
||
|
H (x ) = |
í |
1 |
0 |
||
|
2 |
0, |
||||
|
î |
|||||
4.2. Các kết quả tính toán số
|
x |
> –d |
|
1 |
|
|
x |
£ –d |
|
1 |
|
; |
ìk1 x1 , |
x1 > –d |
|
|
G (x1 ) = í |
, |
x1 £ –d |
|
|
î– k 0 d 0 |
Sau đây ta đi khảo sát rẽ nhánh của nghiệm tuần hoàn trong hệ (9) bằng phương pháp số. Để tính toán số, ta chọn tham số thay đổi là k = k0.10-3, các tham số khác như sau: f0 = 7,8.103(N),
- = 0,4.103(kg), k0 = k.103(N/m), k1 = 0,9.106(N/m), c0 = 0,05.103(Ns/m), c1 = 0,5.103(Ns/m), d = 5.10-3(m), W = 34,56(rad/s).
Hình 2. Biểu đồ rẽ nhánh của hệ (9).
(a) ứng với các nghiệm 2T, 4T, 6T; (b) ứng với các nghiệm 3T, 6T
Tạp chí Khoa học Công nghệ Hàng hải Số 39 – 08/2014 32
Hình 3. Biểu đồ nhân tử Floquet của hệ (9)
(a) với các nghiệm 2T, 4T, 8T; (b) ứng với các nghiệm 3T, 6T
Cho k biến thiên trong khoảng [2; 20], khi đó ta có biểu đồ rẽ nhánh của hệ được cho trên các hình 2. Từ hình vẽ ta thấy, tại k = 20 ứng với điểm A1 trên hình 2a, ta tìm được một nghiệm 2-chu kỳ ổn định. Cho k giảm dần, nghiệm 2-chu kỳ này vẫn ổn định, khi k giảm đến điểm B1 ứng với k = 5,66, tại đây có một nhân tử Floquet đi ra khỏi vòng tròn đơn vị theo hướng -1 (xem hình 3a) nên xuất hiện rẽ nhánh nhân đôi chu kỳ, khi đi qua giá trị này xuất hiện một nghiệm 4-chu kỳ ổn định. Tiếp tục cho k giảm xuống nghiệm 4-chu kỳ vẫn ổn định, khi k giảm đến điểm C1 ứng với k = 3,18, tại đây lại có một nhân tử Floquet đi ra khỏi vòng tròn đơn vị theo hướng -1 (xem hình 3a), do đó lại xuất hiện một rẽ nhánh nhân đôi chu kỳ, khi đi qua giá trị này xuất hiện một nghiệm 8-chu kỳ ổn định. Nghiệm 8-chu kỳ này tồn tại cho đến giá trị k = 2,865. Mặt khác ta thấy, tại điểm A2 trên hình 2b ứng với k = 7,5 xuất hiện một nghiệm 3-chu kỳ song song tồn tại với nghiệm 2-chu kỳ. Nghiệm ba chu kỳ này tồn tại cho đến điểm B2 ứng với k = 2,3, tại đây có một nhân tử Floquet đi ra khỏi vòng tròn đơn vị theo hướng -1 (xem hình 3b), nên xuất hiện một rẽ nhánh nhân đôi chu kỳ, khi đi qua giá trị này nghiệm 6-chu kỳ xuất hiện, nghiệm 6-chu kỳ này tồn tại ổn định cho đến k = 2. Các nghiệm 2-chu kỳ, 4-chu kỳ, 8-chu kỳ, 3-chu kỳ và 6-chu kỳ của hệ (9), tại một số giá trị của k được cho trong các hình 4 – 8.
Hình 4. Nghiệm 2-chu kỳ của hệ (9) tại k = 6,0 Hình 5. Nghiệm 4-chu kỳcủa hệ (9) tại k = 3,2
Hình 6. Nghiệm 8-chu kỳ của hệ (9) tại k = 2,87 Hình 7. Nghiệm 3-chu kỳ của hệ (9) tại k = 2,4
Hình 8. Nghiệm 6-chu kỳ của hệ (9) tại k = 2,0
Tạp chí Khoa học Công nghệ Hàng hải Số 39 – 08/2014 33